What Is the Maximum Height the Blue Ball Reaches
Get the answer to your homework problem.
Try Numerade free for 30 days
University college of engineering
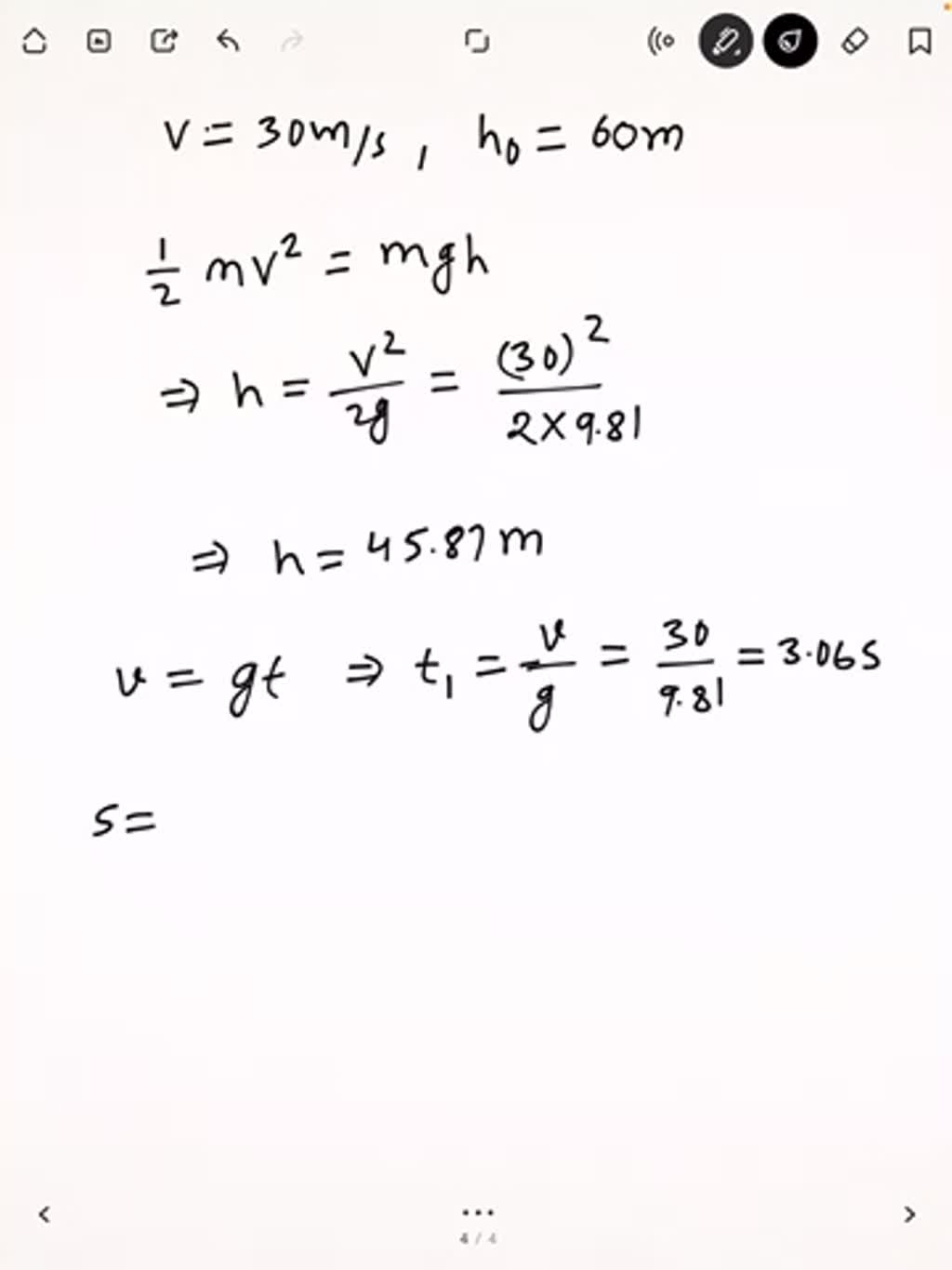
A blue ball is thrown upward with an initial speed of 21.0 m/s, from a height of 0.8 meters above the ground. 2.6 seconds after the blue ball is thrown, a red ball is thrown down with an initial speed of 8.3 m/s from a height of 24.6 meters above the ground. The force of gravity due to the earth results in the balls each having a constant downward acceleration of 9.81 m/s2. 1) What is the maximum height the blue ball reaches? 2) What is the height of the blue ball 1.9 seconds after the red ball is thrown? 3) How long after the red ball is thrown are the two balls in the air at the same height? don't forget to write the answers please! can you help me with this
Related Question
A ball is thrown vertically up with a velocity of $30 \mathrm{m} / \mathrm{s}$ at the edge of a $60-\mathrm{m}$ cliff. Calculate the height $h$ to which the ball rises and the total time $t$ after release for the ball to reach the bottom of the cliff. Neglect air resistance and take the downward acceleration to be $9.81 \mathrm{m} / \mathrm{s}^{2}$
Discussion
You must be signed in to discuss.
Video Transcript
In this question we have speed equals two 30 m/s And initial height has not equals two 60 m. Okay, so using conservation of energy, he can't write one by two M V spare will be equals two MG edge. So from here we get H equals two. We square by two G. We're reaches maximum height. So now substituting the values we get 30 square, there were two multiplayer biggie is 9.81 m per second square. So from here we get H equals to 45.87 m. Okay? So now this is the height from the top of the clip. So the Time for this be accelerating motion will be given by v equals two. Mhm G. D. Okay, so from here we get time T that is steven will be equals to be by G. And We is equal to 30 m/s. Energy is again 9.81. So from here after solving we get 3.06 seconds. Okay, this is the time for the ball to go up. So now the ball bill move freely and it will fall. So the total height it will fall will be s That will be equals two. Edge plus H Nought. So edge is 45.87 plus 60. So that is equal to 105.87 m. Okay, so now the time taken to reach the Call to the bottom of the clip that will be given by as equals two one x 2. GT Square. Where this time? He's safety too. So from here, after rearranging T two comes out to be to us by G Under route. Ok, so now substituting the values we get T two equals two. Too much flab as is this 105.87 divided by G. S. 9.81 under. So from here after solving we get 4.65 seconds. Okay, so the total time T comes out to be even plus T. Two, so T one is equal to 3.6 seconds and T two is equal to 4.65 seconds. So from here total time comes out to be 7.7 seconds. Okay, so this is the answer 40 questions, so this is the time taken and this is the height edge. So these are the two answers for that question.
hodgettsarfeaught.blogspot.com
Source: https://www.numerade.com/ask/question/a-blue-ball-is-thrown-upward-with-an-initial-speed-of-210-ms-from-a-height-of-08-meters-above-the-ground-26-seconds-after-the-blue-ball-is-thrown-a-red-ball-is-thrown-down-with-an-initial-sp-77416/
0 Response to "What Is the Maximum Height the Blue Ball Reaches"
Post a Comment