The Fill Volume of Cans Filled by a Certain Machine Is Normally Distributed

Queslions through 8 The make full volume of cans filled by certain machine normally distributed with hateful Ooz and standard difference Zoz What the probability of one can contain leSs than Ooz"What is the probability Of ane can conlain bclwcen 7502 and [0.1S02?Find the weight such that 99% of cans volition weigh Less than this amountWhat is the probability 0f fQUL cans comprise total more than than 41 02?

Queslions through 8 The fill book of cans filled by certain auto ordinarily distributed with mean Ooz and standard deviation Zoz What the probability of one tin can contain leSs than Ooz" What is the probability Of one can conlain bclwcen 7502 and [0.1S02? Find the weight such that 99% of cans will weigh Less than this amount What is the probability 0f fQUL cans incorporate tOtal more than 41 02?

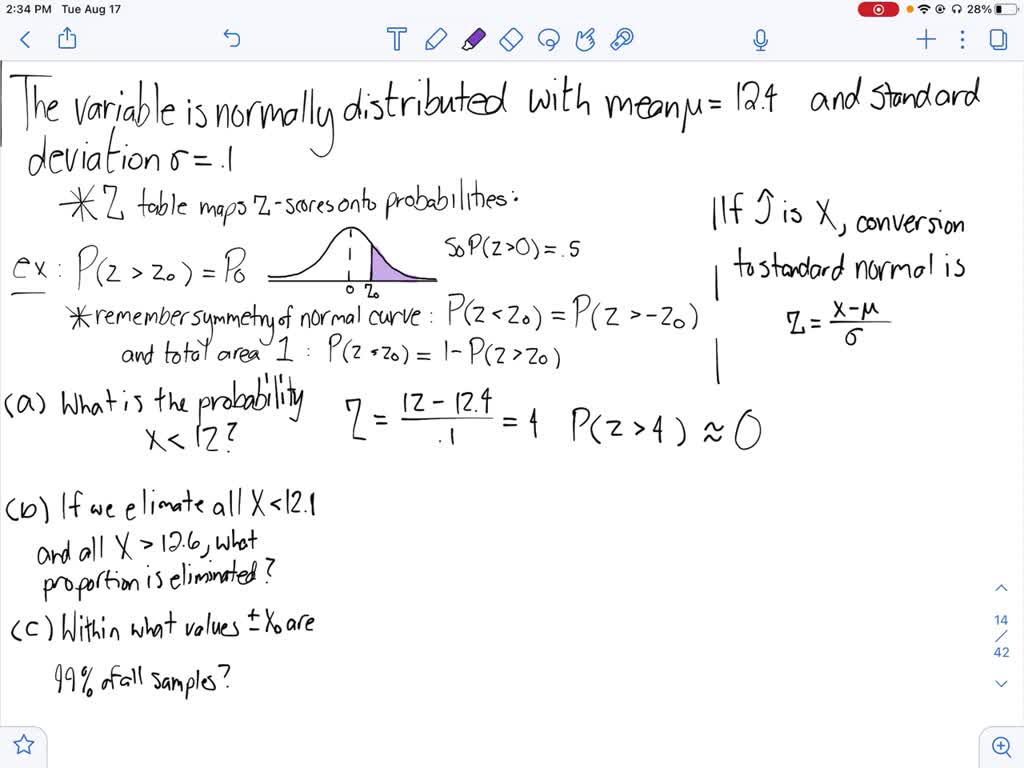
The fill volume of an automated filling machine used for filling cans of carbonated drinkable is normally distributed with a mean of 12.four fluid ounces and a standard deviation of 0.i fluid ounce. (a) What is the probability that a fill up volume is less than 12 fluid ounces? (b) If all cans less than 12.i or greater than 12.6 ounces are scrapped, what proportion of cans is scrapped? (c) Make up one's mind specifications that are symmetric about the mean that include $99 \%$ of all cans.

Right. The random variable is normally distributed with me and new equals 12.four. And standard deviation sigma equals 0.1. Based on this information we want to answer eight receive alot. This question is evaluating our agreement of normal distributions and normally distributed random variables. That's all We rely on. The following relevant information. First and the normal random variable Z z people maps the schools and probabilities. The example here shows that there probably is a greater than nil equals peanut corresponds to an expanse under the standard normal distribution to the correct of that Xena nosotros tin can also practice is the scores less than some donuts. We rely on a symmetry and full expanse of a standard normal attack specifically though because nosotros accept a random variable, that is not piece of cake but rather 10 we have to make the conversion to a standard normal equally equals x minus mu over sigma. This conversion will allow the states to answer a few. See below. Then first, starting with a the probably the X is less than 12 is converting to a Z score the same as the probability Z is less than four. Then because we're looking for the probability is less than four rather than probably is he is greater than four. The solution to this problem will exist rather than zippo, approximately one. This is because of the score of 4 is quite large and and then it is virtually all of the expanse under this. Under normal that is to the left. So adjacent if nosotros eliminate all X less than 12.i and all X greater than 12.6. What proportion is eliminated? This party that we want to answer? What is the area nether the normal bend? To the left? And 12.i is the 1.half-dozen. For standard normal converting to Z scores br formula we accept the wonderful negative three and Z two equals two. That'due south the probability is the left of the ane cluster. Probably easy, greater than C. Two which is ii.241. Finally. To answer part C. We want to answer within what values Plus X 99% of all samples. And then nosotros're looking for the probability that Z is between plus or minus zero equals 00.nine. This is the non equal plus or minus ii.56. That'southward converting to X by inverting our formula here for Z. We have X equals not sigma plus mu or Myu plus or minus two. Sigma equals 12.144. 12.656.

All right, we're talking about, uh, cups getting dispersed, uh, cups getting filled with, um, soft drinks or coffee and a machine. And then on average, it'south gonna make full automatically 7.half-dozen ounces. Just then there'due south a standard divergence of 0.4. So that means nosotros demand to add 0.4 to become get ane standard deviation, which is viii plus another 80.iv is 8.iv, plus some other would be 8.8 ounces. Then we subtract to go get below the standard deviations of seven.2, 6.8 and then 6.four ounces. Okay, So the question the commencement question is, what is the probability of an overflow of eight ounces? So that means probability of information technology existence greater than eight ounces. And so that's going in this direction. So that'south gonna stand for thirteen.5% plus 2.35% plus 0.15 And then that'due south gonna be approximately 16% or 160.xvi question B is asking what would be of it not overflowing. Then the probability of information technology being less than eight would be one minus the 16% that we just gotten political party. So that'southward gonna exist 84% approximately. And so Function C is asking. The machine has been loaded with 850 caps. How many of these do you wait will overflow? So if 16% overflow approximately, that'southward 1.16 of 8 50 meeting we're gonna multiply, and that would exist approximately 136 cups.

And so we know that the vending machine has is dispersing, uh, soft drink into a cup, and it's supposed to be usually distributed and so we can draw the bell shaped curve. And it's supposed to be centered at a hateful of 7.6 ounces with a standard deviation of 0.4 ounces. And then here is where 8 ounces would be one standard departure higher. And we want to know what's the likelihood that the the motorcar volition dispense more than eight ounces because the cup holds viii? And then we want to know what's the likelihood that it's going to manipulate too much liquid? And so it's going to over floor and the cup is full with eight ounces, and so that corresponds with a Z value, one standard deviation college of one. Now we can use on the 98 the 68 95 99.7 rule, or we tin can actually look this value upwardly and permit's just do an approximation. We know that 68% of data in a normal distribution is inside i standard departure, and and then 100% minus 68% gives u.s. 32% and we demand to separate that by two and become sixteen%. And then nosotros know that this region correct in here is approximately sixteen% and this region over here is 16%. So our answer to this question is approximately xvi% volition overflow. And so then our question is, what's the likelihood that information technology won't overflow? And that's the compliment. Then 100% less the approximate 16% is almost an 84% chance of that happening and and so part C as equally if we fail a total of 850 cops. How many of those should end up alluvion while we would anticipate sixteen% of those? And then if we take 16% of viii 50 we would expect that well-nigh 136 of those cups will overflow and we're all set.

Okay, so we know we're going to exist taking 12.0, a which was given equally the ounces of cola. And we're gonna exist subtracting two times 0.iv which is the standard departure, and I'm going to do the same thing. But with addition, 12 point abroad and y'all should go 12 and 12 bespeak sixteen Okay, At present nosotros know that 95% of the data lies between 12 and 12.16 considering we're looking at standard deviation, so nosotros know that nosotros tin can exercise 100% minus 95% divide by two, which is the same thing equally 2.5 percentage. This is just not merely five divided by ii, which is 2.5. So the percentage of cans are less than 12 ounces is going to be ii.5% of Cam's

5 answers

Allow A and B be not-empty sets, and suppose that A = Aj U Az, B = BU Bz where A1, Az, B1, B2z are all non-empty:Evidence that Ax B = (Ax B)U(Ax Bz)(b) Is Ax B = (A, X B) U (Az X B2)? Requite a proof or counter-instance:

Allow A and B be non-empty sets, and suppose that A = Aj U Az, B = BU Bz where A1, Az, B1, B2z are all not-empty: Prove that Ax B = (Ax B)U(Ax Bz) (b) Is Ax B = (A, X B) U (Az X B2)? Give a proof or counter-case:...

five answers

Bi) {3gimt } For the Braph = G beneath:a) Construct a depth-outset spanning tree rooted Jt and using alphabetical ordering half-dozen) Construct & jiff-commencement spanning tree rooted at @ and using alphabetical ordering: c) How many distinct spanning copse does G have? 8) If the edges are assigned weights equally follows: wt(a,b) = 2.wt(a,c) = 3,Wt(b,c) = 3 wt(c,e) = Lwt(d.due east) = 5. wt(d,9) = L wt(d, h) = seven,wt(e f) = 3,Wt(f.[) = 6,wt(g,h) = six,wc(h.0) =3 notice minimal spanning tree

Bi) {3gimt } For the Braph = G below: a) Construct a depth-first spanning tree rooted Jt and using alphabetical ordering six) Construct & breath-first spanning tree rooted at @ and using alphabetical ordering: c) How many distinct spanning copse does G take? 8) If the edges are assigned weights as...

hodgettsarfeaught.blogspot.com

Source: https://itprospt.com/num/2909313/queslions-through-8-the-fill-volume-of-cans-filled-by-certain

Share this post